Общее·количество·просмотров·страницы
четверг, 15 сентября 2011 г.
понедельник, 12 сентября 2011 г.
Задание №1
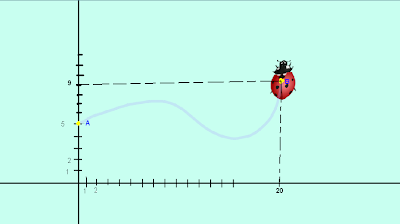
Определение перемещения Божьей Коровки
Цель работы:
· определить проекции перемещения и величины самого перемещение БК
· сравнить путь и перемещение БК
1)
Результаты измерений:
Вектор АВ:
Начальные координаты Конечные координаты
x0=0 x=20
Цель работы:
· определить проекции перемещения и величины самого перемещение БК
· сравнить путь и перемещение БК
1)
Результаты измерений:
Вектор АВ:
Начальные координаты Конечные координаты
x0=0 x=20
y0=5 y=9
Проекции векторов:
Sx=x-x0 Sy=y-y0
Sx=20-0=20 Sy=9-5=4
Длина вектора АВ:
|S| = sqrt (Sx^2 + Sy^2) |S| = sqrt (20^2 + 4^2) = sqrt (416) ≈ 20.3
Sx=x-x0 Sy=y-y0
Sx=20-0=20 Sy=9-5=4
Длина вектора АВ:
|S| = sqrt (Sx^2 + Sy^2) |S| = sqrt (20^2 + 4^2) = sqrt (416) ≈ 20.3
Сравним путь и перемещение:
По графику видно, что путь и перемещение не равны. Путь больше перемещения.
2)
Результаты измерений:
Вектор АВ
Начальные координаты Конечные координаты
x0=3 x=5
y0=10 y=2
Проекции векторов:
Sx=x-x0 Sy=y-y0
Sx=5-3=2 Sy=2-10=-8
Длина вектора АВ:
|S| = sqpt(Sx^2 + Sy^2) |S| = sqrt(2^2 + (-8)^2) = sqrt(68) = 8,2
Сравним путь и перемещение:
По графику видно, что путь и перемещение не равны. Путь больше перемещения.
Результаты измерений:
Вектор АВ
Начальные координаты Конечные координаты
x0=7 x=-3
y0=0,4 y=-3
Проекции векторов:
Sx=x-x0 Sy=y-y0
Sx=-3-7=-10 Sy=-3-0,4=-3,4
Длина вектора АВ:
S| = sqpt(Sx^2 + Sy^2) |S| = sqrt((-10^2) + (-3,4)^2) = sqrt(111,56) = 10,6
По графику видно, что путь и перемещение не равны. Путь больше перемещения.
2)
Результаты измерений:
Вектор АВ
Начальные координаты Конечные координаты
x0=3 x=5
y0=10 y=2
Проекции векторов:
Sx=x-x0 Sy=y-y0
Sx=5-3=2 Sy=2-10=-8
Длина вектора АВ:
|S| = sqpt(Sx^2 + Sy^2) |S| = sqrt(2^2 + (-8)^2) = sqrt(68) = 8,2
Сравним путь и перемещение:
По графику видно, что путь и перемещение не равны. Путь больше перемещения.
Результаты измерений:
Вектор АВ
Начальные координаты Конечные координаты
x0=7 x=-3
y0=0,4 y=-3
Проекции векторов:
Sx=x-x0 Sy=y-y0
Sx=-3-7=-10 Sy=-3-0,4=-3,4
Длина вектора АВ:
S| = sqpt(Sx^2 + Sy^2) |S| = sqrt((-10^2) + (-3,4)^2) = sqrt(111,56) = 10,6
воскресенье, 11 сентября 2011 г.
Задание №2
1) Вектор а
Sx = X - Xo X = 4 Xo = 9 Sx = 4-9 = -5
Sy = Y - Yo Y = -9 Yo = -2 Sy = -9+2 = 7
|S| = sqrt (Sx^2 + Sy^2) |S| = sqrt (-5^2 + 7^2) = sqrt (74) = 8,6
2) Вектор b
Sx = X - Xo X = -4 Xo = -8 Sx = -4 + 8 = 4
Sy = Y - Yo Y = 10 Yo = 5 Sy = 10 - 5 = 5
|S| = sqrt (Sx^2 + Sy^2) |S| = sqrt (4^2 + 5^2) = sqrt (41) = 6,4
3) Сумма векторов a и b
a - b = e
Вектор e
Sx = X - Xo X = 8 Xo = 9 Sx = 8-9 = -1
Вектор e
Sx = X - Xo X = 8 Xo = 9 Sx = 8-9 = -1
Sy = Y - Yo Y = -4Yo = -2 Sy = -4+2 = -2
|S| = sqrt (Sx^2 + Sy^2) |S| = sqrt ((-1^2) + (- 2^2)) = sqrt (5) = 2.2
|S| = sqrt (Sx^2 + Sy^2) |S| = sqrt ((-1^2) + (- 2^2)) = sqrt (5) = 2.2
4) Разность веторов a и b
a - b = e
Вектор e
Sx = X - Xo X = 4Xo =13 Sx = 4-13 = -9
Вектор e
Sx = X - Xo X = 4Xo =13 Sx = 4-13 = -9
Sy = Y - Yo Y = -9 Yo = 3 Sy = -9-3 = -12
|S| = sqrt (Sx^2 + Sy^2) |S| = sqrt ((-9)^2 + (-12^2)) = sqrt (225) = 15
|S| = sqrt (Sx^2 + Sy^2) |S| = sqrt ((-9)^2 + (-12^2)) = sqrt (225) = 15
STAR.
четверг, 8 сентября 2011 г.
Подписаться на:
Комментарии (Atom)